[Java]高能-绝对专业-快速傅立叶变换(FFT/DFT)算法实现

遇到一个通讯专业-波形频谱信号?分析的项目，需要把一组数据做快速傅立叶变换（FTT）后，画出图形(如下图)

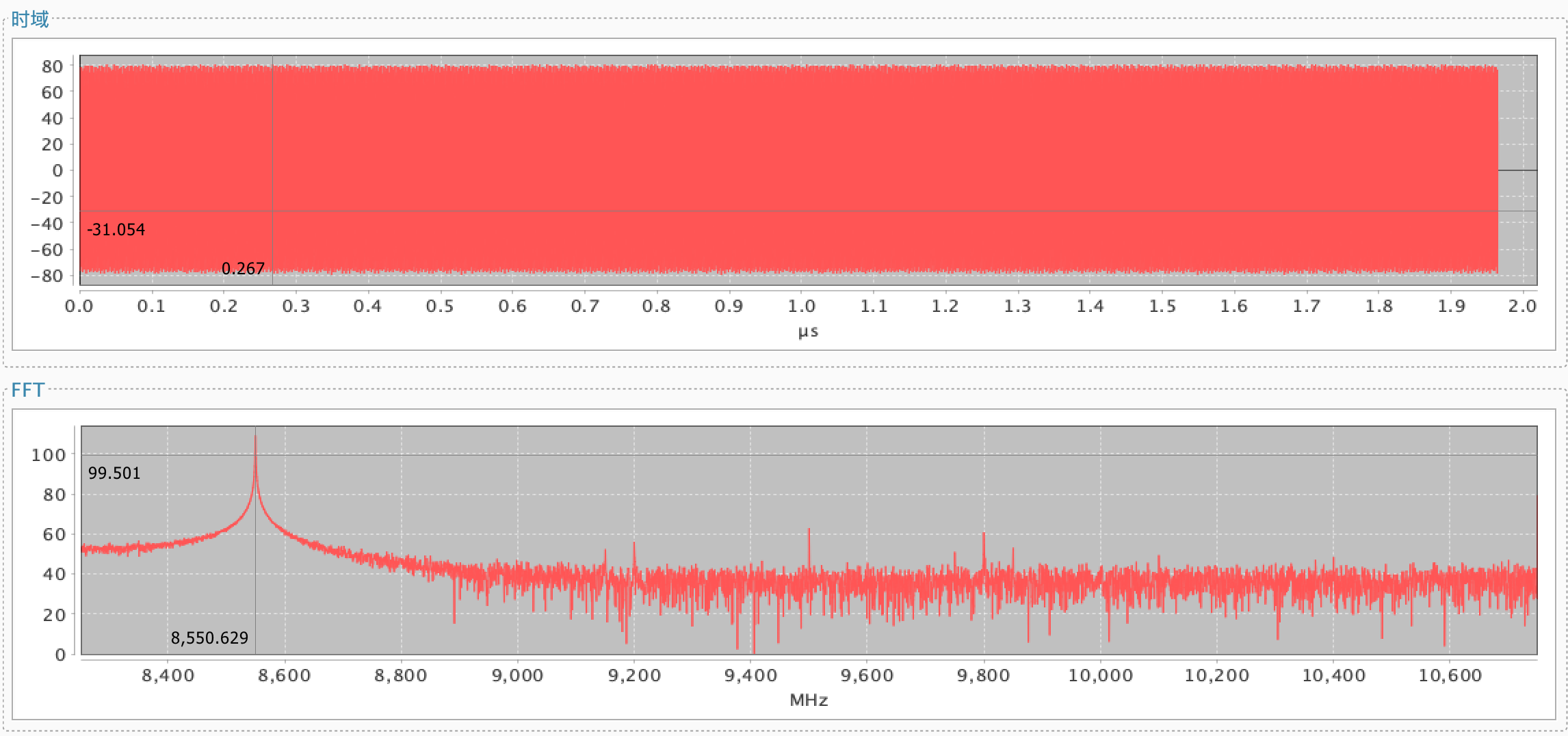
我也不是通信专业的，不懂什么FFT变换，在专业老师的指导下，网上找了相关的算法的代码（如果没有方向，而且专业性特强，很难找），故分享到这里，供有需要的朋友参考。

我一共找到了2个FFT算法，第一个客户说不太对，后来又找到一个，客户说可以了，这边都分享下，供参考选择。

1. 第一套
   
   Java文件 Complex.java

   /**
   * @description 代表一个复数
   */
   public class Complex {
       private final double re;   // the real part 实部
       private final double im;   // the imaginary part 虚部
   
       // create a new object with the given real and imaginary parts 传入实部和虚部，组成一个复数的构造函数
       public Complex(double real, double imag) {
           re = real;
           im = imag;
       }
   
       // return a string representation of the invoking Complex object
       @Override
       public String toString() {
           if (im == 0) return re + "";
           if (re == 0) return im + "i";
           if (im <  0) return re + " - " + (-im) + "i";
           return re + " + " + im + "i";
       }
   
       // return abs/modulus/magnitude and angle/phase/argument
       public double abs()   { return Math.hypot(re, im); }  // Math.sqrt(re*re + im*im)
       public double phase() { return Math.atan2(im, re); }  // between -pi and pi
   
       // return a new Complex object whose value is (this + b)
       public Complex plus(Complex b) {
           Complex a = this;             // invoking object
           double real = a.re + b.re;
           double imag = a.im + b.im;
           return new Complex(real, imag);
       }
   
       // return a new Complex object whose value is (this - b)
       public Complex minus(Complex b) {
           Complex a = this;
           double real = a.re - b.re;
           double imag = a.im - b.im;
           return new Complex(real, imag);
       }
   
       // return a new Complex object whose value is (this * b)
       public Complex times(Complex b) {
           Complex a = this;
           double real = a.re * b.re - a.im * b.im;
           double imag = a.re * b.im + a.im * b.re;
           return new Complex(real, imag);
       }
   
       // scalar multiplication
       // return a new object whose value is (this * alpha)
       public Complex times(double alpha) {
           return new Complex(alpha * re, alpha * im);
       }
   
       // return a new Complex object whose value is the conjugate of this
       public Complex conjugate() {  return new Complex(re, -im); }
   
       // return a new Complex object whose value is the reciprocal of this
       public Complex reciprocal() {
           double scale = re*re + im*im;
           return new Complex(re / scale, -im / scale);
       }
   
       // return the real or imaginary part
       public double re() { return re; }
       public double im() { return im; }
   
       // return a / b
       public Complex divides(Complex b) {
           Complex a = this;
           return a.times(b.reciprocal());
       }
   
       // return a new Complex object whose value is the complex exponential of this
       public Complex exp() {
           return new Complex(Math.exp(re) * Math.cos(im), Math.exp(re) * Math.sin(im));
       }
   
       // return a new Complex object whose value is the complex sine of this
       public Complex sin() {
           return new Complex(Math.sin(re) * Math.cosh(im), Math.cos(re) * Math.sinh(im));
       }
   
       // return a new Complex object whose value is the complex cosine of this
       public Complex cos() {
           return new Complex(Math.cos(re) * Math.cosh(im), -Math.sin(re) * Math.sinh(im));
       }
   
       // return a new Complex object whose value is the complex tangent of this
       public Complex tan() {
           return sin().divides(cos());
       }
   
   
   
       // a static version of plus
       public static Complex plus(Complex a, Complex b) {
           double real = a.re + b.re;
           double imag = a.im + b.im;
           Complex sum = new Complex(real, imag);
           return sum;
       }
   
   
   
       // sample client for testing
       public static void main(String[] args) {
           Complex a = new Complex(5.0, 6.0);
           Complex b = new Complex(-3.0, 4.0);
   
           System.out.println("a            = " + a);
           System.out.println("b            = " + b);
           System.out.println("Re(a)        = " + a.re());
           System.out.println("Im(a)        = " + a.im());
           System.out.println("b + a        = " + b.plus(a));
           System.out.println("a - b        = " + a.minus(b));
           System.out.println("a * b        = " + a.times(b));
           System.out.println("b * a        = " + b.times(a));
           System.out.println("a / b        = " + a.divides(b));
           System.out.println("(a / b) * b  = " + a.divides(b).times(b));
           System.out.println("conj(a)      = " + a.conjugate());
           System.out.println("|a|          = " + a.abs());
           System.out.println("tan(a)       = " + a.tan());
       }
   
   }

   Java文件：FFT.java, FTT变换的测试在main方法里

   public class FFT {
       // compute the FFT of x[], assuming its length is a power of 2
       public static Complex[] fft(Complex[] x) {
           int N = x.length;
   
           // base case
           if (N == 1) return new Complex[] { x[0] };
   
           // radix 2 Cooley-Tukey FFT
           if (N % 2 != 0) { throw new RuntimeException("N is not a power of 2"); }
   
           // fft of even terms
           Complex[] even = new Complex[N/2];
           for (int k = 0; k < N/2; k++) {
               even[k] = x[2*k];
           }
           Complex[] q = fft(even);
   
           // fft of odd terms
           Complex[] odd  = even;  // reuse the array
           for (int k = 0; k < N/2; k++) {
               odd[k] = x[2*k + 1];
           }
           Complex[] r = fft(odd);
   
           // combine
           Complex[] y = new Complex[N];
           for (int k = 0; k < N/2; k++) {
               double kth = -2 * k * Math.PI / N;
               Complex wk = new Complex(Math.cos(kth), Math.sin(kth));
               y[k]       = q[k].plus(wk.times(r[k]));
               y[k + N/2] = q[k].minus(wk.times(r[k]));
           }
           return y;
       }
   
   
       // compute the inverse FFT of x[], assuming its length is a power of 2
       public static Complex[] ifft(Complex[] x) {
           int N = x.length;
           Complex[] y = new Complex[N];
   
           // take conjugate
           for (int i = 0; i < N; i++) {
               y[i] = x[i].conjugate();
           }
   
           // compute forward FFT
           y = fft(y);
   
           // take conjugate again
           for (int i = 0; i < N; i++) {
               y[i] = y[i].conjugate();
           }
   
           // divide by N
           for (int i = 0; i < N; i++) {
               y[i] = y[i].times(1.0 / N);
           }
   
           return y;
   
       }
   
       // compute the circular convolution of x and y
       public static Complex[] cconvolve(Complex[] x, Complex[] y) {
   
           // should probably pad x and y with 0s so that they have same length
           // and are powers of 2
           if (x.length != y.length) { throw new RuntimeException("Dimensions don't agree"); }
   
           int N = x.length;
   
           // compute FFT of each sequence
           Complex[] a = fft(x);
           Complex[] b = fft(y);
   
           // point-wise multiply
           Complex[] c = new Complex[N];
           for (int i = 0; i < N; i++) {
               c[i] = a[i].times(b[i]);
           }
   
           // compute inverse FFT
           return ifft(c);
       }
   
   
       // compute the linear convolution of x and y
       public static Complex[] convolve(Complex[] x, Complex[] y) {
           Complex ZERO = new Complex(0, 0);
   
           Complex[] a = new Complex[2*x.length];
           for (int i = 0;        i <   x.length; i++) a[i] = x[i];
           for (int i = x.length; i < 2*x.length; i++) a[i] = ZERO;
   
           Complex[] b = new Complex[2*y.length];
           for (int i = 0;        i <   y.length; i++) b[i] = y[i];
           for (int i = y.length; i < 2*y.length; i++) b[i] = ZERO;
   
           return cconvolve(a, b);
       }
   
       // display an array of Complex numbers to standard output
       public static void show(Complex[] x, String title) {
           System.out.println(title);
           System.out.println("-------------------");
           for (int i = 0; i < x.length; i++) {
               System.out.println(x[i]);
           }
           System.out.println();
       }
   
   
       /***************************************************************************
        *  Test client and sample execution
        *
        *  % java FFT 4
        *  x
        *  -------------------
        *  -0.03480425839330703
        *  0.07910192950176387
        *  0.7233322451735928
        *  0.1659819820667019
        *
        *  y = fft(x)
        *  -------------------
        *  0.9336118983487516
        *  -0.7581365035668999 + 0.08688005256493803i
        *  0.44344407521182005
        *  -0.7581365035668999 - 0.08688005256493803i
        *
        *  z = ifft(y)
        *  -------------------
        *  -0.03480425839330703
        *  0.07910192950176387 + 2.6599344570851287E-18i
        *  0.7233322451735928
        *  0.1659819820667019 - 2.6599344570851287E-18i
        *
        *  c = cconvolve(x, x)
        *  -------------------
        *  0.5506798633981853
        *  0.23461407150576394 - 4.033186818023279E-18i
        *  -0.016542951108772352
        *  0.10288019294318276 + 4.033186818023279E-18i
        *
        *  d = convolve(x, x)
        *  -------------------
        *  0.001211336402308083 - 3.122502256758253E-17i
        *  -0.005506167987577068 - 5.058885073636224E-17i
        *  -0.044092969479563274 + 2.1934338938072244E-18i
        *  0.10288019294318276 - 3.6147323062478115E-17i
        *  0.5494685269958772 + 3.122502256758253E-17i
        *  0.240120239493341 + 4.655566391833896E-17i
        *  0.02755001837079092 - 2.1934338938072244E-18i
        *  4.01805098805014E-17i
        *
        ***************************************************************************/
   
       public static void main(String[] args) {
           int N = Integer.parseInt(args[0]);
           Complex x[] = new Complex[N];
   
           // original data
           for (int i = 0; i < N; i++) {
               x[i] = new Complex(i, 0);
               x[i] = new Complex(-2*Math.random() + 1, 0);
           }
           show(x, "x");
   
           // FFT of original data
           Complex[] y = fft(x);
           show(y, "y = fft(x)");
   
           // take inverse FFT
           Complex[] z = ifft(y);
           show(z, "z = ifft(y)");
   
           // circular convolution of x with itself
           Complex[] c = cconvolve(x, x);
           show(c, "c = cconvolve(x, x)");
   
           // linear convolution of x with itself
           Complex[] d = convolve(x, x);
           show(d, "d = convolve(x, x)");
       }
   }

2. 上面那套，客户看了生成的图后，感觉说不对，所以又找了一套
   
   新建DFT.java

   /*
    * Free FFT and convolution (Java)
    *
    * Copyright (c) 2017 Project Nayuki. (MIT License)
    * https://www.nayuki.io/page/free-small-fft-in-multiple-languages
    *
    * Permission is hereby granted, free of charge, to any person obtaining a copy of
    * this software and associated documentation files (the "Software"), to deal in
    * the Software without restriction, including without limitation the rights to
    * use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of
    * the Software, and to permit persons to whom the Software is furnished to do so,
    * subject to the following conditions:
    * - The above copyright notice and this permission notice shall be included in
    *   all copies or substantial portions of the Software.
    * - The Software is provided "as is", without warranty of any kind, express or
    *   implied, including but not limited to the warranties of merchantability,
    *   fitness for a particular purpose and noninfringement. In no event shall the
    *   authors or copyright holders be liable for any claim, damages or other
    *   liability, whether in an action of contract, tort or otherwise, arising from,
    *   out of or in connection with the Software or the use or other dealings in the
    *   Software.
    */
   
   /**
    * Downloaded from: https://www.nayuki.io/res/free-small-fft-in-multiple-languages/Fft.java
    */
   
   public class DFT {
       /*
        * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
        * The vector can have any length. This is a wrapper function.
        *
        */
       public static void transform(double[] real, double[] imag) {
           int n = real.length;
           if (n != imag.length)
               throw new IllegalArgumentException("Mismatched lengths");
           if (n == 0)
               return;
           else if ((n & (n - 1)) == 0)  // Is power of 2
               transformRadix2(real, imag);
           else  // More complicated algorithm for arbitrary sizes
               transformBluestein(real, imag);
       }
   
   
       /*
        * Computes the inverse discrete Fourier transform (IDFT) of the given complex vector, storing the result back into the vector.
        * The vector can have any length. This is a wrapper function. This transform does not perform scaling, so the inverse is not a true inverse.
        */
       public static void inverseTransform(double[] real, double[] imag) {
           transform(imag, real);
       }
   
   
       /*
        * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
        * The vector's length must be a power of 2. Uses the Cooley-Tukey decimation-in-time radix-2 algorithm.
        */
       public static void transformRadix2(double[] real, double[] imag) {
           // Length variables
           int n = real.length;
           if (n != imag.length)
               throw new IllegalArgumentException("Mismatched lengths");
           int levels = 31 - Integer.numberOfLeadingZeros(n);  // Equal to floor(log2(n))
           if (1 << levels != n)
               throw new IllegalArgumentException("Length is not a power of 2");
   
           // Trigonometric tables
           double[] cosTable = new double[n / 2];
           double[] sinTable = new double[n / 2];
           for (int i = 0; i < n / 2; i++) {
               cosTable[i] = Math.cos(2 * Math.PI * i / n);
               sinTable[i] = Math.sin(2 * Math.PI * i / n);
           }
   
           // Bit-reversed addressing permutation
           for (int i = 0; i < n; i++) {
               int j = Integer.reverse(i) >>> (32 - levels);
               if (j > i) {
                   double temp = real[i];
                   real[i] = real[j];
                   real[j] = temp;
                   temp = imag[i];
                   imag[i] = imag[j];
                   imag[j] = temp;
               }
           }
   
           // Cooley-Tukey decimation-in-time radix-2 FFT
           for (int size = 2; size <= n; size *= 2) {
               int halfsize = size / 2;
               int tablestep = n / size;
               for (int i = 0; i < n; i += size) {
                   for (int j = i, k = 0; j < i + halfsize; j++, k += tablestep) {
                       int l = j + halfsize;
                       double tpre = real[l] * cosTable[k] + imag[l] * sinTable[k];
                       double tpim = -real[l] * sinTable[k] + imag[l] * cosTable[k];
                       real[l] = real[j] - tpre;
                       imag[l] = imag[j] - tpim;
                       real[j] += tpre;
                       imag[j] += tpim;
                   }
               }
               if (size == n)  // Prevent overflow in 'size *= 2'
                   break;
           }
       }
   
   
       /*
        * Computes the discrete Fourier transform (DFT) of the given complex vector, storing the result back into the vector.
        * The vector can have any length. This requires the convolution function, which in turn requires the radix-2 FFT function.
        * Uses Bluestein's chirp z-transform algorithm.
        */
       public static void transformBluestein(double[] real, double[] imag) {
           // Find a power-of-2 convolution length m such that m >= n * 2 + 1
           int n = real.length;
           if (n != imag.length)
               throw new IllegalArgumentException("Mismatched lengths");
           if (n >= 0x20000000)
               throw new IllegalArgumentException("Array too large");
           int m = Integer.highestOneBit(n) * 4;
   
           // Trignometric tables
           double[] cosTable = new double[n];
           double[] sinTable = new double[n];
           for (int i = 0; i < n; i++) {
               int j = (int) ((long) i * i % (n * 2));  // This is more accurate than j = i * i
               cosTable[i] = Math.cos(Math.PI * j / n);
               sinTable[i] = Math.sin(Math.PI * j / n);
           }
   
           // Temporary vectors and preprocessing
           double[] areal = new double[m];
           double[] aimag = new double[m];
           for (int i = 0; i < n; i++) {
               areal[i] = real[i] * cosTable[i] + imag[i] * sinTable[i];
               aimag[i] = -real[i] * sinTable[i] + imag[i] * cosTable[i];
           }
           double[] breal = new double[m];
           double[] bimag = new double[m];
           breal[0] = cosTable[0];
           bimag[0] = sinTable[0];
           for (int i = 1; i < n; i++) {
               breal[i] = breal[m - i] = cosTable[i];
               bimag[i] = bimag[m - i] = sinTable[i];
           }
   
           // Convolution
           double[] creal = new double[m];
           double[] cimag = new double[m];
           convolve(areal, aimag, breal, bimag, creal, cimag);
   
           // Postprocessing
           for (int i = 0; i < n; i++) {
               real[i] = creal[i] * cosTable[i] + cimag[i] * sinTable[i];
               imag[i] = -creal[i] * sinTable[i] + cimag[i] * cosTable[i];
           }
       }
   
   
       /*
        * Computes the circular convolution of the given real vectors. Each vector's length must be the same.
        */
       public static void convolve(double[] x, double[] y, double[] out) {
           int n = x.length;
           if (n != y.length || n != out.length)
               throw new IllegalArgumentException("Mismatched lengths");
           convolve(x, new double[n], y, new double[n], out, new double[n]);
       }
   
   
       /*
        * Computes the circular convolution of the given complex vectors. Each vector's length must be the same.
        */
       public static void convolve(double[] xreal, double[] ximag,
                                   double[] yreal, double[] yimag, double[] outreal, double[] outimag) {
   
           int n = xreal.length;
           if (n != ximag.length || n != yreal.length || n != yimag.length
                   || n != outreal.length || n != outimag.length)
               throw new IllegalArgumentException("Mismatched lengths");
   
           xreal = xreal.clone();
           ximag = ximag.clone();
           yreal = yreal.clone();
           yimag = yimag.clone();
           transform(xreal, ximag);
           transform(yreal, yimag);
   
           for (int i = 0; i < n; i++) {
               double temp = xreal[i] * yreal[i] - ximag[i] * yimag[i];
               ximag[i] = ximag[i] * yreal[i] + xreal[i] * yimag[i];
               xreal[i] = temp;
           }
           inverseTransform(xreal, ximag);
   
           for (int i = 0; i < n; i++) {  // Scaling (because this FFT implementation omits it)
               outreal[i] = xreal[i] / n;
               outimag[i] = ximag[i] / n;
           }
       }
   }

   调用举例

   private void drawFFTChart() {
       //用FFT.java做好像有问题，现在用DFT.java做
   //        int n = findN();
   //        Complex source[] = new Complex[n];
   //        log.info("fft sample num: " + n + ", source sample num: " + ifData.length);
   
       int ifDataLength = ifData.length;
       double[] real = new double[ifDataLength]; // 实部
       double[] imag = new double[ifDataLength]; // 虚部
       for (int i = 0; i < ifDataLength; i++) {
           real[i] = ifData[i];
       }
       DFT.transform(real, imag);
       int fftLength = ifDataLength / 2;
       double[] fftData = new double[fftLength];
       for (int i = 0; i < fftLength; i++) {
           double abs = Math.hypot(real[i], imag[i]);
           fftData[i] = 20D * Math.log10(abs);
       }
       ((IFFFTChartPane) fftChartPanel).updateChartData(fftData);
   }